FIR The Frequency Sampling Method 実験 Java
FIRのLPFとHPFを設計してみて、もう少し高度なことをやってみたくなった。ということで、日曜日はThe Frequency Sampling Methodにチャレンジ。特徴としてはLPFやHPFに比べ自由度の高いフィルターが作れるというところ。周波数ごとにフィルターを掛ける割合を微調整できるので、グラフィックイコライザーやパラメトリックイコライザーのようなことが実現できる。解像度を上げていけば市販品をしのぐことも夢ではない。LPF/HPFと同じようにJavaでデジタルフィルタ用の係数を出力するところまで、つまりインパルス応答を得るまで作る。
これを実現するにはフーリエ変換を勉強しないと手が出ない。以前勉強したのだが、すっかり忘れた。またちょっとメモを読み返したりして再勉強。
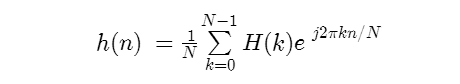
結論としては、IDFT(離散フーリエ逆変換)の式をプログラミングすることで、実現できそうだ。あとは、やりながら考えるのが手っ取り早い。細かな部分まで完全に理解しようとすると数年かかりそうなので、厳密さは無視して、ガンガンとプログラムを組んでみる。それにしても、この手の日本語情報は少ないなぁ。うまく見つけられないだけなのか? 結局下の英語ページを読みながら、プログラムをする。
http://cnx.org/content/m28292/latest/
h(n)がFIRのタップの係数に相当する。この(n)は無限大個数あるのが理想。でも当然無理なので、オーディオの場合は最低でも数百とかにする。LPFならもっと少なくても良いのだが、HPFを考慮するとまだ足りない。今回はサンプリング周波数44100Hzのオーディオファイルを使う。低域もきれいに加工したいので、タップ数は1万ぐらい欲しくなる。さらに直線位相特性などを考慮すると、その2倍というところだ。ということで2万程度で実験した。
H(k)は周波数域を分解したそれぞれの係数。Hには任意の0~1.0を入れる。自分が欲しい周波数特性をここでコントロールする。(k)を増やすと分解能が上がるので細かく周波数をいじることができる。今回は22050個にした。つまり扱える周波数を22050分割。サンプリング周波数44100Hzの場合、扱える周波数は22050Hzまでなので1Hz単位で制御できることになる。
式にeとかiがある。この手の専門教育を受けていないので、ちょっとしり込みする部分。 有名なオイラーの公式を使って、式を実部と虚部に分けることにする。虚数は数学的には i を使うし、電気の世界では j を使う。私は使い分けが出来ていないので混在している。
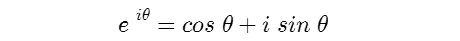
今回は直線位相特性ということで、虚部は0になるので、使っているのはcosの実部だけ。これで周波数領域を時間領域へ変換する。

ある程度プログラムが動くようになると、今度は意図した係数が出るまで調整の連続。プログラムのおバカな修正を繰り返して、やっと完成。窓関数はHammingを使用した。とりあえず、お試し的に作っただけの、みっともないソースは非公開。イコライジング方法はユーザーインターフェイス的に、いろいろ考えられるが、今回はLPFでもHPFでもないところを示せればよいので、1行コードで楕円状の周波数特性を実現しようと思う。
楕円の式
この式から周波数特性が半楕円を描くようにしたい。
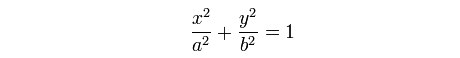
式を変形させていく。今回はyのマイナスはいらないので、プラスだけ導くようにした。また0Hzから20kHzにかけて半楕円を描くようにプログラム。係数をwavファイルとして書き出して、Audacityで読み込む。そのインパルス応答は以下のようなものになった。これだけ見て、LPFとHPFぽさを感じたら、かなりのFIR通。

そのインパルス応答の周波数スペクトルはきれいな半楕円。対数表示で楕円に見せるのはちょっと計算が面倒なので、リニア表示。

下はホワイトノイズに上記を畳み込み。VSTのSIRで畳み込んだ。結果としては、そこそこの精度で楕円が実現できた。これだけの精度でフィルターを掛けられるのなら文句ないなぁ。
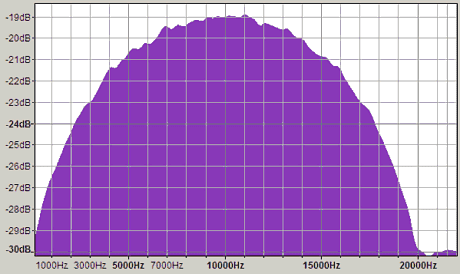
今回はフーリエ変換の応用ということで、プログラムしてみただけで、これを実用レベルにまで作りこむ気はない。処理スピードの向上とか、GUIはハードルが高いからね。むしろ原理的なことが知りたいだけなので、あれこれ、初歩的な実験をしていこうかと思う。
sound programming 目次はこちら
これを実現するにはフーリエ変換を勉強しないと手が出ない。以前勉強したのだが、すっかり忘れた。またちょっとメモを読み返したりして再勉強。
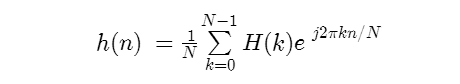
結論としては、IDFT(離散フーリエ逆変換)の式をプログラミングすることで、実現できそうだ。あとは、やりながら考えるのが手っ取り早い。細かな部分まで完全に理解しようとすると数年かかりそうなので、厳密さは無視して、ガンガンとプログラムを組んでみる。それにしても、この手の日本語情報は少ないなぁ。うまく見つけられないだけなのか? 結局下の英語ページを読みながら、プログラムをする。
http://cnx.org/content/m28292/latest/
h(n)がFIRのタップの係数に相当する。この(n)は無限大個数あるのが理想。でも当然無理なので、オーディオの場合は最低でも数百とかにする。LPFならもっと少なくても良いのだが、HPFを考慮するとまだ足りない。今回はサンプリング周波数44100Hzのオーディオファイルを使う。低域もきれいに加工したいので、タップ数は1万ぐらい欲しくなる。さらに直線位相特性などを考慮すると、その2倍というところだ。ということで2万程度で実験した。
H(k)は周波数域を分解したそれぞれの係数。Hには任意の0~1.0を入れる。自分が欲しい周波数特性をここでコントロールする。(k)を増やすと分解能が上がるので細かく周波数をいじることができる。今回は22050個にした。つまり扱える周波数を22050分割。サンプリング周波数44100Hzの場合、扱える周波数は22050Hzまでなので1Hz単位で制御できることになる。
式にeとかiがある。この手の専門教育を受けていないので、ちょっとしり込みする部分。 有名なオイラーの公式を使って、式を実部と虚部に分けることにする。虚数は数学的には i を使うし、電気の世界では j を使う。私は使い分けが出来ていないので混在している。
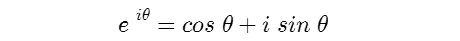
今回は直線位相特性ということで、虚部は0になるので、使っているのはcosの実部だけ。これで周波数領域を時間領域へ変換する。

ある程度プログラムが動くようになると、今度は意図した係数が出るまで調整の連続。プログラムのおバカな修正を繰り返して、やっと完成。窓関数はHammingを使用した。とりあえず、お試し的に作っただけの、みっともないソースは非公開。イコライジング方法はユーザーインターフェイス的に、いろいろ考えられるが、今回はLPFでもHPFでもないところを示せればよいので、1行コードで楕円状の周波数特性を実現しようと思う。
楕円の式
この式から周波数特性が半楕円を描くようにしたい。
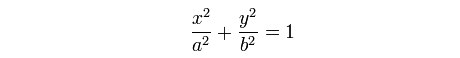
式を変形させていく。今回はyのマイナスはいらないので、プラスだけ導くようにした。また0Hzから20kHzにかけて半楕円を描くようにプログラム。係数をwavファイルとして書き出して、Audacityで読み込む。そのインパルス応答は以下のようなものになった。これだけ見て、LPFとHPFぽさを感じたら、かなりのFIR通。

そのインパルス応答の周波数スペクトルはきれいな半楕円。対数表示で楕円に見せるのはちょっと計算が面倒なので、リニア表示。

下はホワイトノイズに上記を畳み込み。VSTのSIRで畳み込んだ。結果としては、そこそこの精度で楕円が実現できた。これだけの精度でフィルターを掛けられるのなら文句ないなぁ。

今回はフーリエ変換の応用ということで、プログラムしてみただけで、これを実用レベルにまで作りこむ気はない。処理スピードの向上とか、GUIはハードルが高いからね。むしろ原理的なことが知りたいだけなので、あれこれ、初歩的な実験をしていこうかと思う。
sound programming 目次はこちら
