All-pass filterの実験 Java
オールパスフィルター(All-pass filter)ってちょっと不思議。振幅をいじらず、特定の周波数を中心に位相だけを反転するフィルター。何に使うの?という感じだが、フェイザーというエフェクトを調べていたら、オールパスフィルターを使っていたので、まずはこの原理を理解することから始めたいと思う。
AudacityのNyquistにもオールパスのコマンドはあった。
(allpass2 signal hz [q])
というもので、具体的には
(allpass2 s 1000 1)
こんな感じで使う。Effect メニューの Nyquist Prompt に以下のように入力するだけで実行できる。
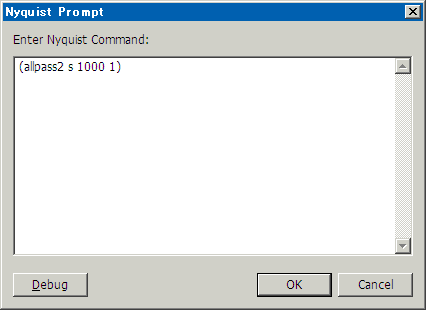
sは選択範囲のサウンドで、1000は反転したい周波数。単位はHz。1はその影響する範囲。とりあえず、これを使って加工してみる。100Hzから15000Hzのチャープ信号を作る。拡大すると下のような波形で、低いサイン波から始まって、段々と周波数が上がっていくもの。
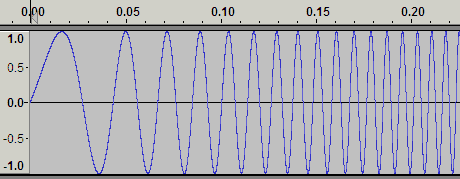
この信号に (allpass2 s 1000 1) コマンドを通す。出来たサウンドは何の変化も感じられない。聴いても同じようにしか聴こえない。でも拡大してみると、ちゃんと1000Hzで位相が反転しているのが分かる。
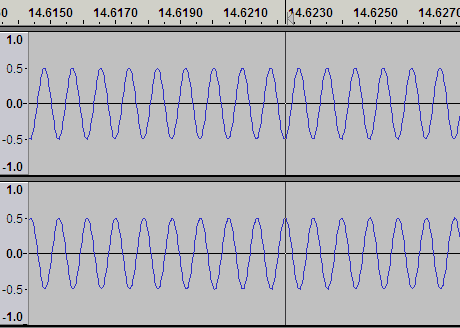
さらにオリジナルのチャープ信号と合成すると明らかになる。1000Hzは位相が反転しているので、打ち消しあって、振幅は0になる。他の周波数は位相が揃っているので、2倍の振幅になっている。

ということで、オールパスフィルタのイメージがつかめたところで、数式から追ってみることにする。最終的にはIIRの2次で実現してみようかと思う。ブロック図はこれを採用する。

オールパスの数式を探してみる。WIKIだと、アナログに関して書かれているが、ちょっとこれからの変換はイメージできない。もう少し調べると、Robert Bristow-Johnsonという人が書いた「Cookbook formulae for audio EQ biquad filter coefficients」を利用している人が多いようだ。確かに2次のbiquadが一通り書かれているので、そのまま使えば簡単に実現できるようだ。そのままコピーも面白くないので、自分で計算することにした。でも下記の式だけは参考にさせてもらった。
H(s) = (s^2 - s/Q + 1) / (s^2 + s/Q + 1)
この式を変形することからスタート。まずは見やすくしてみた。

Qはフィルタの効き具合を調整する。式の上では1/Qというのもなんか気持ち悪いので、とりあえず、
1/Q = Q
として計算している。どういう解釈がよいのか分からないので、計算が楽な方向で適当に調整しています。最後につじつま合わせをすればよい。さらに下のように置き換える。
s = s / 2π * fc
2π * fc = A
この fc は中心周波数で、その中身は以下のようになる。
fc = tan ( π * cutoff / sfreq ) / (2 * π )
cutoff = カットオフ周波数 位相を反転したい周波数
sfreq = 音声ファイルのサンプリング周波数 44100Hzなど
それぞれを上記の式に入れて整理し、最後に、
s = ((1-z)/(1+z))
に置き換えて係数を求めると下のような式になる。手でやっていると目がチカチカして結構書き間違えるので、Maximaでさくっと計算してしまう。分母が a の係数で、分子が b の係数となる。

分母は a の係数でこうなる。
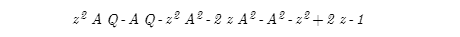
分子は、先頭にマイナスがあるので全部掛けてしまえばいい。整理すると以下のようになる。これが b の係数になる。

これらが次数ごとに各係数となる。Zが付かない 1 や AQ などは0次で、z が付くものは1次。z^2 が付くものは2次となる。整理すると以下のようになる。
a0 = -A^2 - AQ -1
a1 = -2*A^2 +2
a2 = -A^2 +AQ -1
b0 = -A^2 + AQ -1
b1 = -2*A^2 +2
b2 = -A^2 - AQ -1
これらが係数になるのだが、上記ブロック図に入れるには細工が必要。そもそもa0が入るところがないので、a0を1にする必要がある。ということで、すべての係数をa0で割ってしまえばいい。またaの係数はa0以外すべて-1を掛ける必要がある。これはそもそもブロック図に書かれていることも多い。Javaで係数を求めるプログラムは以下のようになった。見通しをよくするために、順に手を加えてみた。このプログラムにcutoff(カットオフ周波数)と、sfreq(サンプリング周波数)を入力すれば、各係数が求められる。Qも本来は他のクラスから渡す値だけど、ここでは0.70710678118655という数値を入れて、1/Qで計算した上で係数計算に使用している。Qが大きくなるほど効きが鋭くなる。
試しにカットオフ周波数1000Hzでサンプリング周波数44100Hzで計算させると、係数は以下のようになる。
a0= 1.0
a1= 1.7990964094846686
a2= -0.8175124033847586
b0= 0.8175124033847586
b1= -1.7990964094846686
b2= 1.0
この係数を使って、チャープ信号を加工して、オリジナルとミックスしてみると以下のようになった。周波数スペクトルで見てもちゃんと1000Hzが落ち込んでいる。まずは成功というところか。

Qの値を π にしてみた。効きは鋭くなり、プラスマイナス1オクターブ以内が落ち込むようになる。

ちなみにAudacityの(allpass2 signal hz [q])と比較したら、Qの値と効き方は一致するので、間違いはなさそうだ。しかしAudacityのAll-passは周波数ポイントが高域側にわずかにズレる・・・。自作はジャストで効いている。
さて、Phaserの予備実験が出来たので、次は本体の製作に入りたいところだが、仕事が忙しくなりそうなので、しばらくBlogは休むかもしれない。
sound programming 目次
AudacityのNyquistにもオールパスのコマンドはあった。
(allpass2 signal hz [q])
というもので、具体的には
(allpass2 s 1000 1)
こんな感じで使う。Effect メニューの Nyquist Prompt に以下のように入力するだけで実行できる。

sは選択範囲のサウンドで、1000は反転したい周波数。単位はHz。1はその影響する範囲。とりあえず、これを使って加工してみる。100Hzから15000Hzのチャープ信号を作る。拡大すると下のような波形で、低いサイン波から始まって、段々と周波数が上がっていくもの。

この信号に (allpass2 s 1000 1) コマンドを通す。出来たサウンドは何の変化も感じられない。聴いても同じようにしか聴こえない。でも拡大してみると、ちゃんと1000Hzで位相が反転しているのが分かる。

さらにオリジナルのチャープ信号と合成すると明らかになる。1000Hzは位相が反転しているので、打ち消しあって、振幅は0になる。他の周波数は位相が揃っているので、2倍の振幅になっている。

ということで、オールパスフィルタのイメージがつかめたところで、数式から追ってみることにする。最終的にはIIRの2次で実現してみようかと思う。ブロック図はこれを採用する。

オールパスの数式を探してみる。WIKIだと、アナログに関して書かれているが、ちょっとこれからの変換はイメージできない。もう少し調べると、Robert Bristow-Johnsonという人が書いた「Cookbook formulae for audio EQ biquad filter coefficients」を利用している人が多いようだ。確かに2次のbiquadが一通り書かれているので、そのまま使えば簡単に実現できるようだ。そのままコピーも面白くないので、自分で計算することにした。でも下記の式だけは参考にさせてもらった。
H(s) = (s^2 - s/Q + 1) / (s^2 + s/Q + 1)
この式を変形することからスタート。まずは見やすくしてみた。

Qはフィルタの効き具合を調整する。式の上では1/Qというのもなんか気持ち悪いので、とりあえず、
1/Q = Q
として計算している。どういう解釈がよいのか分からないので、計算が楽な方向で適当に調整しています。最後につじつま合わせをすればよい。さらに下のように置き換える。
s = s / 2π * fc
2π * fc = A
この fc は中心周波数で、その中身は以下のようになる。
fc = tan ( π * cutoff / sfreq ) / (2 * π )
cutoff = カットオフ周波数 位相を反転したい周波数
sfreq = 音声ファイルのサンプリング周波数 44100Hzなど
それぞれを上記の式に入れて整理し、最後に、
s = ((1-z)/(1+z))
に置き換えて係数を求めると下のような式になる。手でやっていると目がチカチカして結構書き間違えるので、Maximaでさくっと計算してしまう。分母が a の係数で、分子が b の係数となる。

分母は a の係数でこうなる。
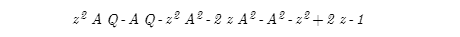
分子は、先頭にマイナスがあるので全部掛けてしまえばいい。整理すると以下のようになる。これが b の係数になる。

これらが次数ごとに各係数となる。Zが付かない 1 や AQ などは0次で、z が付くものは1次。z^2 が付くものは2次となる。整理すると以下のようになる。
a0 = -A^2 - AQ -1
a1 = -2*A^2 +2
a2 = -A^2 +AQ -1
b0 = -A^2 + AQ -1
b1 = -2*A^2 +2
b2 = -A^2 - AQ -1
これらが係数になるのだが、上記ブロック図に入れるには細工が必要。そもそもa0が入るところがないので、a0を1にする必要がある。ということで、すべての係数をa0で割ってしまえばいい。またaの係数はa0以外すべて-1を掛ける必要がある。これはそもそもブロック図に書かれていることも多い。Javaで係数を求めるプログラムは以下のようになった。見通しをよくするために、順に手を加えてみた。このプログラムにcutoff(カットオフ周波数)と、sfreq(サンプリング周波数)を入力すれば、各係数が求められる。Qも本来は他のクラスから渡す値だけど、ここでは0.70710678118655という数値を入れて、1/Qで計算した上で係数計算に使用している。Qが大きくなるほど効きが鋭くなる。
double fc = Math.tan(Math.PI*cutoff/sfreq)/(2*Math.PI); double A= 2*Math.PI*fc; double Q= 1/0.70710678118655; a[0]= -1*Math.pow(A, 2) -(A*Q) -1.0; a[1]= -2*Math.pow(A, 2) +2.0; a[2]= -1*Math.pow(A, 2) +(A*Q) -1.0; b[0]= -1*Math.pow(A, 2) +(A*Q) -1.0; b[1]= -2*Math.pow(A, 2) +2.0; b[2]= -1*Math.pow(A, 2) -(A*Q) -1.0; a[1]= a[1]/a[0]; a[2]= a[2]/a[0]; b[0]= b[0]/a[0]; b[1]= b[1]/a[0]; b[2]= b[2]/a[0]; a[0]= 1.0; a[1]= -1*a[1]; a[2]= -1*a[2]; |
a0= 1.0
a1= 1.7990964094846686
a2= -0.8175124033847586
b0= 0.8175124033847586
b1= -1.7990964094846686
b2= 1.0
この係数を使って、チャープ信号を加工して、オリジナルとミックスしてみると以下のようになった。周波数スペクトルで見てもちゃんと1000Hzが落ち込んでいる。まずは成功というところか。

Qの値を π にしてみた。効きは鋭くなり、プラスマイナス1オクターブ以内が落ち込むようになる。

ちなみにAudacityの(allpass2 signal hz [q])と比較したら、Qの値と効き方は一致するので、間違いはなさそうだ。しかしAudacityのAll-passは周波数ポイントが高域側にわずかにズレる・・・。自作はジャストで効いている。
さて、Phaserの予備実験が出来たので、次は本体の製作に入りたいところだが、仕事が忙しくなりそうなので、しばらくBlogは休むかもしれない。
sound programming 目次
