音律について
ドレミの誕生
現代のドレミの基盤を作ったのはピタゴラス(教団)。なんと紀元前500年以上前に、その基礎は出来上がっていた。では、どうやってドレミを作り出したのか?オクターブは基準
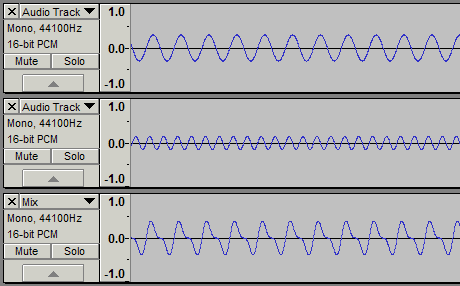
まず、ある音に対して最も調和する音を探してみる。これはピタゴラスに限らず、世界中の共通の認識でオクターブの音となる。低い「A(ラ)」に最も馴染む音は、高い「A」もしくは、さらに低い「A」ということになる。実際に波形を作って音にしてみた。純粋なサイン波の「A 440Hz」に対して途中でオクターブ上の「A 880Hz」をミックスしたサンプル。880Hzは耳に付くので、-6dB音量を下げている。実際に聴いてみると、響きとしては単純な印象で、ハーモニーという感じはない。きわめて近い関係の音である。波形を見るとよく分かる。上段が440Hzで、中段が880Hz、下段がミックスしたもの。オクターブ上の音は周期がちょうど1/2になり、ミックスしてもうなりは生じず、安定した波形になっている。
現代の最も使われているドレミは、オクターブを均等に12分割している平均律という音律。でもピタゴラスの時代は、同じ12分割でも、微妙にいろいろ違う。ピタゴラスが、その12音を作り出す過程を追ってみる。
弦の倍音
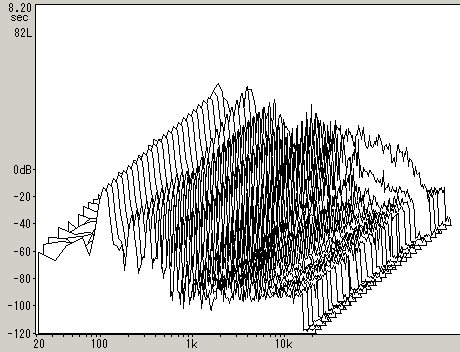
はじめに弦の振動の分析から始まる。まずは実際のギターで音を出してみる。5弦開放のA(110Hz)の音。弦を鳴らすと、いくつもの倍音が鳴っていることが分かる。Audacity(波形編集ソフト)を使って、周波数スペクトルで視覚的に確認してみる。

一番低い音が基音のA110Hzの音で最もピークが大きい。これでAの音が鳴っていると人は認識できる。明らかなピークとして存在する倍音を順に並べると以下のようになった。
基音 110Hz A
2倍音 220Hz A
3倍音 331Hz E
4倍音 440Hz A
5倍音 551Hz C#
6倍音 659Hz E
7倍音 770Hz G
8倍音 880Hz A
・
・
・
スペクトルを見ても、かなりたくさんの音で構成されているのが分かる。ピークの大きさが様々であり、時間軸で見ると、鳴り続けている音もあれば、すぐに減衰する音もある。弦が鳴っている音以外にアタック音もあるので、かなりの高次倍音が含まれている。倍音の周波数は物理的な条件があるので計算どおりではない。これらを総合してギターらしい音色ということになる。
和音的に見ていくとルートと5度の音が中心に構成されていて、若干長3度も感じる。つまりメジャーコードが一番近い。メジャーコードが基本的なコードとして扱われている理由がこういうところにあったりする。
C1をルートとして順次倍音を重ねていくとどうなるかという実験をしてみる。 ただ、手抜きの理由から、純粋な倍音ではなく、平均律の音を使ってみた。(平均律と純粋な倍音には結構ズレがある。) 音色は倍音を含まないサイン波を利用する。これは加算式シンセと同じやり方とも言える。音量は高次倍音になるほど下げている。
結果的には和音とも音色とも言えない印象だが、本当の純粋倍音で音量も調整していくと、音色という感じになるはずだ。 面白いのは倍音を見ていくと、どういう音が、どういう順で出現してくるのかという点。下のようになっている。
C1 C2 G2 C3 E3 G3 Bb3 C4 D4 E4 F#4 G4 A4 Bb4 B4 C5 c#5 D5 Eb5 E5 〇 F5 F#5 G5 G#5 A5 〇 A#5 B5 〇 C6
Cを基準にしているので、CとGがよく出現するのはわかるのだが、4オクターブ以上になると12音すべてが順番に出現しているのがわかる。さらに〇い部分は音サンプルに含まなかった音なのだが、これは半音ではない1/4音など。下の音域は支配的であるが、上は割と自由度が高いと言える。
興味深いのはBbとかが早々に出現するところや、D、F#あたりだろう。Cのメジャースケールから考えると、BbとF#はちょっと待ったがかかりそうだ。しかしブルースなどではF#の減5度をブルーノートとして使っているので、なるほどと思えてきたりする。
対数を利用する
音に関しては絶対的な物理量(振動数)よりも対数で考えた方が理解しやすい。音に対する人間の感覚は対数的である。例としてオクターブの関係を見るとよく分かる。110、220、440、880、1760Hzのサイン波を合成したものを周波数スペクトルで表示してみる。横軸を振動数Hz(リニア)で見ると、オクターブ間隔は周波数の通りで等間隔ではない。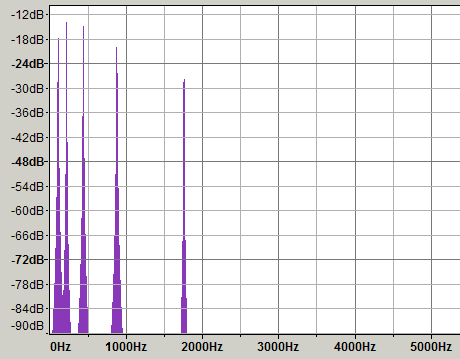
これを対数にすると、
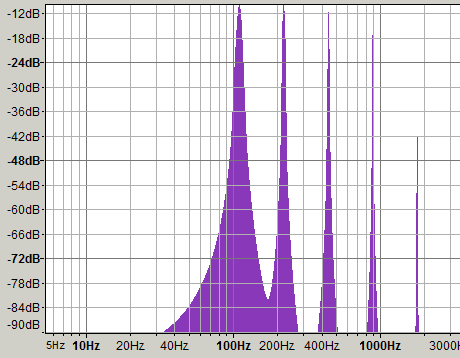
オクターブの間隔は等間隔になってしまう。例えば1オクターブの範囲を平行移動しても常に1オクターブを示せる。リニア表示ではそうはいかない。人間の感覚としては、やっぱりオクターブは等間隔だろう。何かと対数は便利なのだ。
振動を視覚的に確認
次に、弦を弾いたときの振動を絵にするとこうなる。x軸の0がギターのナットで、piがギターのサドルと考えればよい。ちなみにpi/2は12フレットに相当する。まずは最も大きく低い音である基音。ギターではフレットからブリッジまでのめいっぱいの振動がこれに相当する。

2倍音は、中心は振動していない。基音に対して1オクターブ高い音になる。

3倍音は1/3地点が振動していない。基音に対して1オクターブと5度高い音になっている。

4倍音は基音に対して2オクターブ高い音になる。
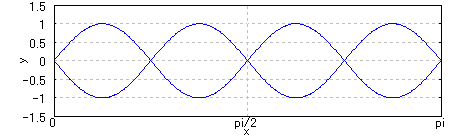
同じように高次倍音になっていく。
ギターでは、その倍音だけを鳴らすテクニックもある。ハーモニックスと言って、振動しない部分に指を触れることで実現できる。2倍音なら弦の真ん中に触れ、3倍音なら1/3の箇所に触れるという具合。実際にやってみる。5弦開放110Hzから6倍音まで。
この倍音に着目して音律を作リ出したのがピタゴラス
1本の弦を弾いただけで、たくさんの倍音が自然に発生する。ここに含まれる倍音は基音と最も調和すると考えるのは自然なこと。ピタゴラスが特に着目したのは3倍音。オクターブ以外で基音と最も調和する倍音として3倍音を選んだ。基音に対して1オクターブと完全5度高い音だ。確かにオクターブ以外の倍音で、基音から最も近いのが3倍音であり、6倍音も3倍音と同じ完全5度の音が含まれている。他に5倍音の長3度の音も比較的近いが、3倍音ほどの主張はない。なので第一候補というのは頷ける。ピタゴラスは基音と3倍音との調和から、次のようにして音律を作り出した。とりあえずここでは、具体的な周波数で計算してみる。まず、基音をA110Hzとする。
次に、その基音の3倍音330Hzを定める。
次に、その3倍音の3倍音990Hzを定める。
さらに、その3倍音の3倍音2970Hzを定める。
さらに・・・というように繰り返していく。そうするとAから始めた場合は以下のようになるのだが、すぐに可聴域を超えて超音波になってしまうので、オクターブ内に納まるように修正する。
| 音 | 3倍音 Hz |
オクターブ修正 Hz |
| A | 110 | 110 |
| E | 330 | 165 |
| B | 990 | 123.75 |
| F# | 2970 | 185.625 |
| C# | 8910 | 139.21875 |
| G# | 26730 | 208.828125 |
| D# | 80190 | 156.62109375 |
| A# | 240570 | 117.4658203125 |
| F | 721710 | 176.19873046875 |
| C | 2165130 | 132.1490478515625 |
| G | 6495390 | 198.22357177734375 |
| D | 19486170 | 148.6676788330078125 |
| A | 58458510 | 223.00151824951171875 |
上記の計算はプログラムを組んで計算している。せっかくなので、JavaScriptに移植してBlog上でも計算できるようにしてみた。基音(fundamental tone)を入力するとオクターブ上までの12音の周波数を計算して表示する。
音の低い順に並べ替えて再生するとこのようになる。
次に馴染深いアイオニアン・スケール(ドレミファソラシド)をAから出してみる、聴きなれているドレミとなんか違う。
このままでは現代の平均律の12音階とは違う、周波数を比較してみる。
| 音 | ピタゴラス Hz |
平均律 Hz |
ズレ cent |
| A | 110 | 110 | 0 |
| E | 165 | 164.81378 | +1.96 |
| B | 123.75 | 123.47083 | +3.91 |
| F# | 185.625 | 184.99721 | +5.87 |
| C# | 139.21875 | 138.59132 | +7.82 |
| G# | 208.828125 | 207.65235 | +9.78 |
| D# | 156.62109375 | 155.56349 | +11.73 |
| A# | 117.4658203125 | 116.54094 | +13.68 |
| F | 176.19873046875 | 174.61412 | +15.64 |
| C | 132.1490478515625 | 130.81278 | +17.5 |
| G | 198.22357177734375 | 195.99772 | +19.55 |
| D | 148.6676788330078125 | 146.83238 | +21.51 |
| A | 223.00151824951171875 | 220 | +23.46 |
ピタゴラス音律の和音サンプル
単純なコードI-V7-Iをピタゴラス音律で作るとこんなかんじ。具体的なコードはF-C7-Fにした。純粋なサイン波の合成なので、和音として濁ってしまう箇所がいくつか確認できる。波形のかたちを見ると緩やかにうなりがある。

純正律の和音サンプル
より響きを良くしたいということで、改良され、様々な音律が生まれる。有名なのは純正律だろうか。単純な整数比で作られいる。オクターブ内の周波数比は以下の通り。
1/1,9/8,5/4,4/3,3/2,5/3,15/8,2/1
最も和音の響きがきれいということだが、転調できないという欠点がある。 といういことで純正律のサンプル和音。コード進行は同じ。純正律は和音にしても、全くうなりがないのが分かる。面倒なのはキーに合わせて、それぞれの音を調整する必要がある。今回はF-C7-Fという進行なのでキーはFになっている。Fは平均律のA=440Hzから計算した174.61412Hzを基準にした。現在なら完全コンピュータ制御で純正律もありかも。シンセ限定になってしまうつまらなさはあるが・・・

平均律の和音サンプル
その後、和音の響きを妥協し、1オクターブを均等に12分割した平均律が誕生。キーが変わっても、比は全く変わらないメリットがある。転調が自在に出来るということで、現在は平均律が主流。波形を見ると常時安定して?小刻みにうなっているが、生楽器では大抵気にならない。すぐに減衰するギターでは全く問題ないレベル。というかギターは音律よりも、構造的にもっと大きな問題を抱えていて、平均律さえもちゃんと実現できていないのが現状。

音律を調べてみて
今回最も興味深かったのは、3倍音を導く過程で得た音の並び方。A,E,B,F#,C#,G#,D#,A#,F,C,G,Dこの並びは何かと重要。音楽理論的には、5度上昇もしくは4度下降となる。これはコード進行の最も基本的な進行。
また初めの5回まで繰り返した音は A E B F# C#。これを長音階のドレミに置き換えると C G D A E となり、さらに並べなおすと、C D E G A となり、よくある5音階になる。民族的な音楽ではこの5音階がよく出てくる。素朴なメロディは、はじめの5音を使っていることがわかる。もちろん理論的にそうなったのではなく、自然に心地よいと思える音が、この5音になったということ。5度上昇を繰り返していくと、計算結果からも明らかだが、段々と誤差が蓄積されていく。キーとなる音から、あまり遠い音を使うのは無理が出てくるのかもしれない。
また普通のドレミのスケールはCから始めた場合の7音かと思いきや、そうでもなかったりする。Cからやってしまうと、Fは#してしまうのだ。実はピタゴラスの時代はFが#した音階(リディアン・スケール)の方がポピュラーだったとか。現代のCから始まるドレミ、つまりアイオニアン・スケールがポピュラーになったのは完全4度が入っていて便利だからのようだ。
以上で音律の実験はおしまい
音楽的には、この音律の導き方から、様々なヒントが得られる。多くのメロティやコードの秘密がここにあると言っても過言ではない。人が自然に感じる心地よい音の流れっていうのが、実は物理的な見方で明確になることも多い。それにしても、音楽理論で言う度数って非合理的。基音を1度としているところから、間違ってしまったという感じ。現代だったら0度だろう。そして、4度とか5度、さらに短7度とか、長3度などの呼び方は個人的にありえない・・・ 半音を無視した並びで呼ぶので、計算がやりにくいったらありゃしない・・・ 音楽教育を受けていない人間にとって違和感ありまくり。各音を0~11度で呼んでもらえたら、何かと便利だったのに。ということで個人的には0~11を使ったりする。イメージとしてはアナログ時計のような考え方を使っている。基音が12時で完全4度が5時、完全5度が7時という具合。他の人に勧める気はないが、自作プログラムでも内部的に、これらを使っている。素直に計算ができるのでね。ちなみに音楽的な呼び方はこんなかんじ。
完全1度
短2度
長2度
短3度
長3度
完全4度
減5度
完全5度
短6度
長6度
短7度
長7度
完全8度
そしてギターのフレットを見たら、「これぞ合理的!」 と思ったよ。開放=0フレットで、1,2,3...フレットと半音ごとに理想的な呼び方がされている。12フレットは0フレットのオクターブ上の音になる。原始的な楽器のはずなのに、現代のテクノロジーとも調和できる下地がある。ギターは素晴らしいよ。構造的に問題だらけだけど。
中学生ぐらいから学ぶフーリエ変換 目次はこちら
