IIR デジタルフィルタ Javaで自作
少ないタップ数で実現できる IIR (Infinite impulse response 無限インパルス応答)デジタルフィルタ。LPF/HPF(ローパス/ハイパスフィルタ)でも試しに作ってみようかと思う。図書館で借りた本を頼りにプログラムまで作ることにしてみた。
これまでに作ったFIRはタップ数が多く計算量が増えてしまうのに対して、IIRは極端にタップ数が少なく1~8程度。無限のフィードバックを利用することで少ないタップを実現している。欠点は位相のズレが出てしまうことと、条件によっては不安定になりやすいことなど。AudacityのLPF/HPFはIIRのButterworthを使っているので、いろいろ試したら欠点はやはり位相だと思えた。元の波形が結構大きく変化してしまう。FIRで同じようにLPF/HPFを作ると、波形の乱れはなかった。その差は歴然。ただIIRは計算量が少ないので、ディレイやリバーブ内のLPFとして使う場合には都合がよい。
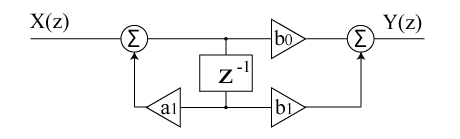
IIRは元々アナログ回路用のフィルタなので、アナログ回路設計を雛形にしてデジタルに変換するという設計が基本のようだ。IIRで作れる有名なフィルタは Butterworth、Chebyshev、楕円フィルタなどがある。実際使いそうなフィルタは平坦な特性のButterworthぐらいなので、これだけ試すことにした。基本となるブロック図は以下のようなもの。図は4次のブロック図。このan、bnに係数を入れることでフィルタになる。anはフィードバックになる。さらにカスケードするなどの改良型もある。

内容を理解しようとしたら、結構難しいかも。まずは下の式から次数ごとのバターワースのプロトタイプというものを作る。
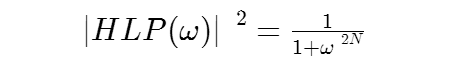
とりあえず1次から4次までのプロトタイプは数式でこのようになった。
1次
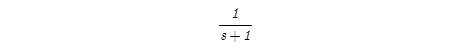
2次

3次

4次

次に求めたい特性に応じて、どの次数のButterworthを使えばよいかを計算する。Butterworthはカットオフ周波数が-3dBになるように計算されている。単純に次数が増えれば急な傾斜を実現できる。軽く高域を削る程度なら1次でよいこともあるし、完全なカットをしたいなら4次でも不十分になる。ちなみにAudacityでは1次、2次、4次、6次、8次のButterworth HPF/LPFが用意されている。
上記はアナログ回路でも共通の部分。次にデジタルフィルタ用に変換する必要がある。どうもその方法がいろいろあるようだ・・・。単純にデジタルプロトタイプに変換することにした。やることは上記 s に次の式を代入するだけ。
HPF: (2πfc) / ((z-1)/(z+1))
LPF: ((z-1)/(z+1)) / (2πfc)
fcの中はこんなかんじ。ωcはカットオフ周波数で、fsはサンプリング周波数。
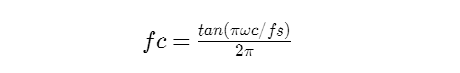
とりあえずHPFを作る。代入して計算すると分母がanで、分子がbnで、次数ごとにタップの係数として使用する。そのとき、a0を1にするために、すべての係数をa0で割る。また、ブロック図に書く場合も多いようだが、aの係数にはa0以外は-1をかけている。サンプリング周波数44100Hzのときカットオフを100Hzで計算した結果は以下の通り。LPFの場合は係数の値は、このままにして、bnをすべてプラスにすれば実現できる。
a0= 1.0
a1= 3.9627669835998334
a2= -5.888992488169376
a3= 3.8896765255622308
a4= -0.9634510614418316
b0= 0.9815554411733295
b1= -3.926221764693318
b2= 5.889332647039977
b3= -3.926221764693318
b4= 0.9815554411733295
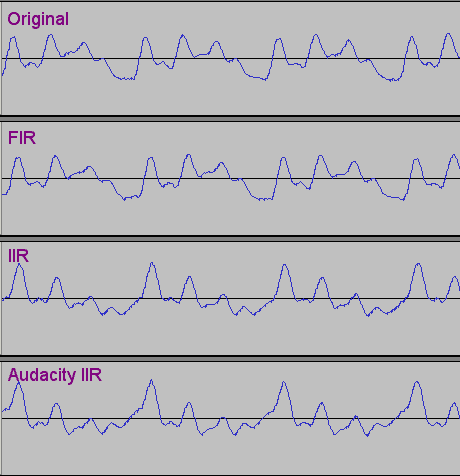
IIRのブロック図をそのままプログラムして係数を入れて実験。意外と簡単に目標を達成できた。ちゃんと100Hzでカットできている。AudacityのButterworthと比較しても差はあまりない。悪い意味でButterworthらしい傾向もそのまま。下はホワイトノイズにHPFをかけてみたところ。カットオフは100Hz。

Butterworthを使うと、位相の問題が出てしまう。下の波形を見ると分かるが、オリジナル波形が割りとプラスマイナス対称なのに対して、Butterworthを通すとプラス側に傾く傾向にある。詳細は不明だが、Audacityも自作IIRも同じ傾向なのでButterworthの問題なのだろう。ちなみにFIRのタップ数2000ぐらいで同じように100Hzでカットしてみると、オリジナル波形に酷似している。波形を拡大しても全く崩れていない。音質重視ならFIRだなと思ったよ。

波形の拡大。オリジナルとFIRはかなり近い波形。一方Butterworth自作とAudacityは同じ傾向。
1次Butterworthもやってみる
下の式だけを頼りに適当に作ったので、かなり怪しい。まず1次のブロック図が本にもなく、ネットで検索してもほとんど見かけない。
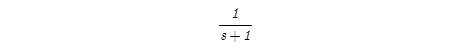
ブロック図はいくつかの方法があるようだが、4次の場合と同じようにしたかったので下図を採用した。
実際に音声ファイルに適用してみる。サンプリング周波数44100Hzのホワイトノイズを加工している。LPFは1000Hzでカット。AudacityのLPFよりもきれいに出ている。でたらめソースを公開するのは忍びないので、係数だけ書くとこうなる。これもa0を1にするためにすべての係数をa0で割っている。あとはa1にマイナスを掛けている。
a0= 1.0
a1= 0.8667884394996352
b0= 0.06660578025018238
b1= 0.06660578025018238

HPFも1000Hzでカット。たった1個のタップで、よくここまでカットできると関心。こんなんでカットオフ周波数も調整できるHPFとしてちゃんと機能しているところが不思議。LPFと係数も似通っている。bが*10ということと、b1の符号が反転しているだけ。
a0= 1.0
a1= 0.8667884394996352
b0= 0.6660578025018238
b1= -0.6660578025018238

2次 Butterworthも作ってみた
係数を求める計算に慣れたので、実用的そうな2次も作ってみた。ブロック図はこんな感じで、上の4次、1次と同じようにa0なしにした。計算から動かすところまで20分ぐらいで完成。式の展開はMaximaを使った。手ではさすがに面倒くさいので。各次数とLPF/HPFの切替プログラムまで作って、実際の音声ファイルをスムーズに加工できるようにした。これでIIRの実験は終了。

同じようにサンプリング周波数44100Hzで、カットオフ周波数1000Hzの場合の係数はこのようになった。すべての係数をa0で割って、a1、a2に-1を掛けているのは同じ。
LPF
a0= 1.0
a1= 1.7990964094846686
a2= -0.8175124033847586
b0= 0.004603998475022465
b1= 0.00920799695004493
b2= 0.004603998475022465
HPF
a0= 1.0
a1= 1.7990964094846686
a2= -0.8175124033847586
b0= 0.9041522032173568
b1= -1.8083044064347136
b2= 0.9041522032173568
実際に作ってみた感想としては、FIRに比べ計算量が圧倒的に少なく、高速に処理したいときには便利そうだ。リバーブやディレイのLPFとして好都合に思えた。ただ理論は難解で、係数の計算はかなり面倒。フィルタ係数の参考例がなく正しいかどうかのチェックもできていない。仕方なく実際フィルタとして機能するかどうかで判断した。細部はいろいろ間違ってそうだが、やりたいことは実現できているので、これらを使っていこうと思う。
sound programming 目次はこちら
これまでに作ったFIRはタップ数が多く計算量が増えてしまうのに対して、IIRは極端にタップ数が少なく1~8程度。無限のフィードバックを利用することで少ないタップを実現している。欠点は位相のズレが出てしまうことと、条件によっては不安定になりやすいことなど。AudacityのLPF/HPFはIIRのButterworthを使っているので、いろいろ試したら欠点はやはり位相だと思えた。元の波形が結構大きく変化してしまう。FIRで同じようにLPF/HPFを作ると、波形の乱れはなかった。その差は歴然。ただIIRは計算量が少ないので、ディレイやリバーブ内のLPFとして使う場合には都合がよい。
IIRは元々アナログ回路用のフィルタなので、アナログ回路設計を雛形にしてデジタルに変換するという設計が基本のようだ。IIRで作れる有名なフィルタは Butterworth、Chebyshev、楕円フィルタなどがある。実際使いそうなフィルタは平坦な特性のButterworthぐらいなので、これだけ試すことにした。基本となるブロック図は以下のようなもの。図は4次のブロック図。このan、bnに係数を入れることでフィルタになる。anはフィードバックになる。さらにカスケードするなどの改良型もある。

内容を理解しようとしたら、結構難しいかも。まずは下の式から次数ごとのバターワースのプロトタイプというものを作る。
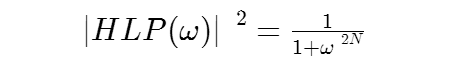
とりあえず1次から4次までのプロトタイプは数式でこのようになった。
1次
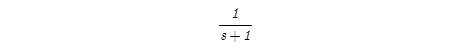
2次

3次

4次

次に求めたい特性に応じて、どの次数のButterworthを使えばよいかを計算する。Butterworthはカットオフ周波数が-3dBになるように計算されている。単純に次数が増えれば急な傾斜を実現できる。軽く高域を削る程度なら1次でよいこともあるし、完全なカットをしたいなら4次でも不十分になる。ちなみにAudacityでは1次、2次、4次、6次、8次のButterworth HPF/LPFが用意されている。
上記はアナログ回路でも共通の部分。次にデジタルフィルタ用に変換する必要がある。どうもその方法がいろいろあるようだ・・・。単純にデジタルプロトタイプに変換することにした。やることは上記 s に次の式を代入するだけ。
HPF: (2πfc) / ((z-1)/(z+1))
LPF: ((z-1)/(z+1)) / (2πfc)
fcの中はこんなかんじ。ωcはカットオフ周波数で、fsはサンプリング周波数。
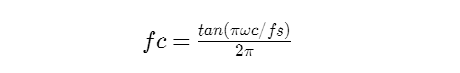
とりあえずHPFを作る。代入して計算すると分母がanで、分子がbnで、次数ごとにタップの係数として使用する。そのとき、a0を1にするために、すべての係数をa0で割る。また、ブロック図に書く場合も多いようだが、aの係数にはa0以外は-1をかけている。サンプリング周波数44100Hzのときカットオフを100Hzで計算した結果は以下の通り。LPFの場合は係数の値は、このままにして、bnをすべてプラスにすれば実現できる。
a0= 1.0
a1= 3.9627669835998334
a2= -5.888992488169376
a3= 3.8896765255622308
a4= -0.9634510614418316
b0= 0.9815554411733295
b1= -3.926221764693318
b2= 5.889332647039977
b3= -3.926221764693318
b4= 0.9815554411733295
IIRのブロック図をそのままプログラムして係数を入れて実験。意外と簡単に目標を達成できた。ちゃんと100Hzでカットできている。AudacityのButterworthと比較しても差はあまりない。悪い意味でButterworthらしい傾向もそのまま。下はホワイトノイズにHPFをかけてみたところ。カットオフは100Hz。

Butterworthを使うと、位相の問題が出てしまう。下の波形を見ると分かるが、オリジナル波形が割りとプラスマイナス対称なのに対して、Butterworthを通すとプラス側に傾く傾向にある。詳細は不明だが、Audacityも自作IIRも同じ傾向なのでButterworthの問題なのだろう。ちなみにFIRのタップ数2000ぐらいで同じように100Hzでカットしてみると、オリジナル波形に酷似している。波形を拡大しても全く崩れていない。音質重視ならFIRだなと思ったよ。

波形の拡大。オリジナルとFIRはかなり近い波形。一方Butterworth自作とAudacityは同じ傾向。

1次Butterworthもやってみる
下の式だけを頼りに適当に作ったので、かなり怪しい。まず1次のブロック図が本にもなく、ネットで検索してもほとんど見かけない。
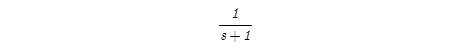
ブロック図はいくつかの方法があるようだが、4次の場合と同じようにしたかったので下図を採用した。

実際に音声ファイルに適用してみる。サンプリング周波数44100Hzのホワイトノイズを加工している。LPFは1000Hzでカット。AudacityのLPFよりもきれいに出ている。でたらめソースを公開するのは忍びないので、係数だけ書くとこうなる。これもa0を1にするためにすべての係数をa0で割っている。あとはa1にマイナスを掛けている。
a0= 1.0
a1= 0.8667884394996352
b0= 0.06660578025018238
b1= 0.06660578025018238

HPFも1000Hzでカット。たった1個のタップで、よくここまでカットできると関心。こんなんでカットオフ周波数も調整できるHPFとしてちゃんと機能しているところが不思議。LPFと係数も似通っている。bが*10ということと、b1の符号が反転しているだけ。
a0= 1.0
a1= 0.8667884394996352
b0= 0.6660578025018238
b1= -0.6660578025018238

2次 Butterworthも作ってみた
係数を求める計算に慣れたので、実用的そうな2次も作ってみた。ブロック図はこんな感じで、上の4次、1次と同じようにa0なしにした。計算から動かすところまで20分ぐらいで完成。式の展開はMaximaを使った。手ではさすがに面倒くさいので。各次数とLPF/HPFの切替プログラムまで作って、実際の音声ファイルをスムーズに加工できるようにした。これでIIRの実験は終了。

同じようにサンプリング周波数44100Hzで、カットオフ周波数1000Hzの場合の係数はこのようになった。すべての係数をa0で割って、a1、a2に-1を掛けているのは同じ。
LPF
a0= 1.0
a1= 1.7990964094846686
a2= -0.8175124033847586
b0= 0.004603998475022465
b1= 0.00920799695004493
b2= 0.004603998475022465
HPF
a0= 1.0
a1= 1.7990964094846686
a2= -0.8175124033847586
b0= 0.9041522032173568
b1= -1.8083044064347136
b2= 0.9041522032173568
実際に作ってみた感想としては、FIRに比べ計算量が圧倒的に少なく、高速に処理したいときには便利そうだ。リバーブやディレイのLPFとして好都合に思えた。ただ理論は難解で、係数の計算はかなり面倒。フィルタ係数の参考例がなく正しいかどうかのチェックもできていない。仕方なく実際フィルタとして機能するかどうかで判断した。細部はいろいろ間違ってそうだが、やりたいことは実現できているので、これらを使っていこうと思う。
sound programming 目次はこちら
