FFTによるconvolution(畳み込み)実験
「DFTによる畳み込み」記事と同じ内容をFFTでもやってみた。
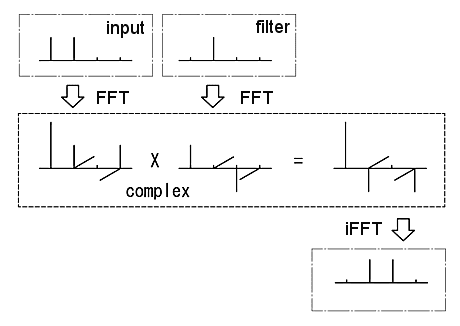
内容は下図の通りで、1,1,0,0 の4つの入力信号と 0,1,0,0 のフィルタを、それぞれFFT(高速フーリエ変換)して周波数領域にしてしまう。そして周波数領域で複素数の乗算をして、iFFT(逆高速フーリエ変換)で戻すというもの。フィルタの内容は1サンプル遅れるディレイなので、結果は 0,1,1,0 となり、時間軸での畳み込みと同じ結果が出る。
FFTで重要なのはサンプル数が2^nであるということ。今回は4という少ないサンプル数で試している。
この記事の例はサンプル数が少なすぎて、現実感がない。実際の入力信号は、かなり長いのが普通だし、リアルタイムであれば、長さが不明ということになる。フィルタは普通数千サンプルぐらいで、長くても数万サンプル。この長さの違うサンプルを畳み込む必要がある。その方法は overlap-add method という畳み込み手法で、次回の記事で書いてみたいと思う。この方法を使えば、高速なFIRデジタルフィルタを実現できる。実際に多くのエフェクトで利用されている。Audacity の Equlaization や Convolution Reverb などがよい例。
コンパイルして実行すると以下のような結果が表示される。1サンプル遅れているのが確認できる。
sound programming 目次はこちら
FFTで重要なのはサンプル数が2^nであるということ。今回は4という少ないサンプル数で試している。

この記事の例はサンプル数が少なすぎて、現実感がない。実際の入力信号は、かなり長いのが普通だし、リアルタイムであれば、長さが不明ということになる。フィルタは普通数千サンプルぐらいで、長くても数万サンプル。この長さの違うサンプルを畳み込む必要がある。その方法は overlap-add method という畳み込み手法で、次回の記事で書いてみたいと思う。この方法を使えば、高速なFIRデジタルフィルタを実現できる。実際に多くのエフェクトで利用されている。Audacity の Equlaization や Convolution Reverb などがよい例。
FFT convolution 実験用ソースコード
|
N: FFT1 Real FFT1 Imaginary FFT1 Power 0: 2.00000000000 0.00000000000 2.00000000000 1: 1.00000000000 -1.00000000000 1.41421356237 2: 0.00000000000 0.00000000000 0.00000000000 3: 1.00000000000 1.00000000000 1.41421356237 N: FFT2 Real FFT2 Imaginary FFT2 Power 0: 1.00000000000 0.00000000000 1.00000000000 1: 0.00000000000 -1.00000000000 1.00000000000 2: -1.00000000000 0.00000000000 1.00000000000 3: -0.00000000000 1.00000000000 1.00000000000 N: convolution R convolution i 0: 2.00000000000 0.00000000000 1: -1.00000000000 -1.00000000000 2: 0.00000000000 0.00000000000 3: -1.00000000000 1.00000000000 N: iFFT Real iFFT Imaginary 0: 0.00000000000 0.00000000000 1: 1.00000000000 0.00000000000 2: 1.00000000000 -0.00000000000 3: 0.00000000000 -0.00000000000 |
sound programming 目次はこちら
